Quantum entanglement with Q#
- Classical bits hold a single binary value such as a 0 or 1, the state of a qubit can be in a superposition of two quantum states, 0 and 1. Each possible quantum state has an associated probability amplitude.
- The act of measuring a qubit produces a binary result, either 0 or 1, with a certain probability, and changes the state of the qubit out of superposition.
- Multiple qubits can be entangled such that they cannot be described independently from each other. That is, whatever happens to one qubit in an entangled pair also happens to the other qubit.
We will see this in step wise manner-
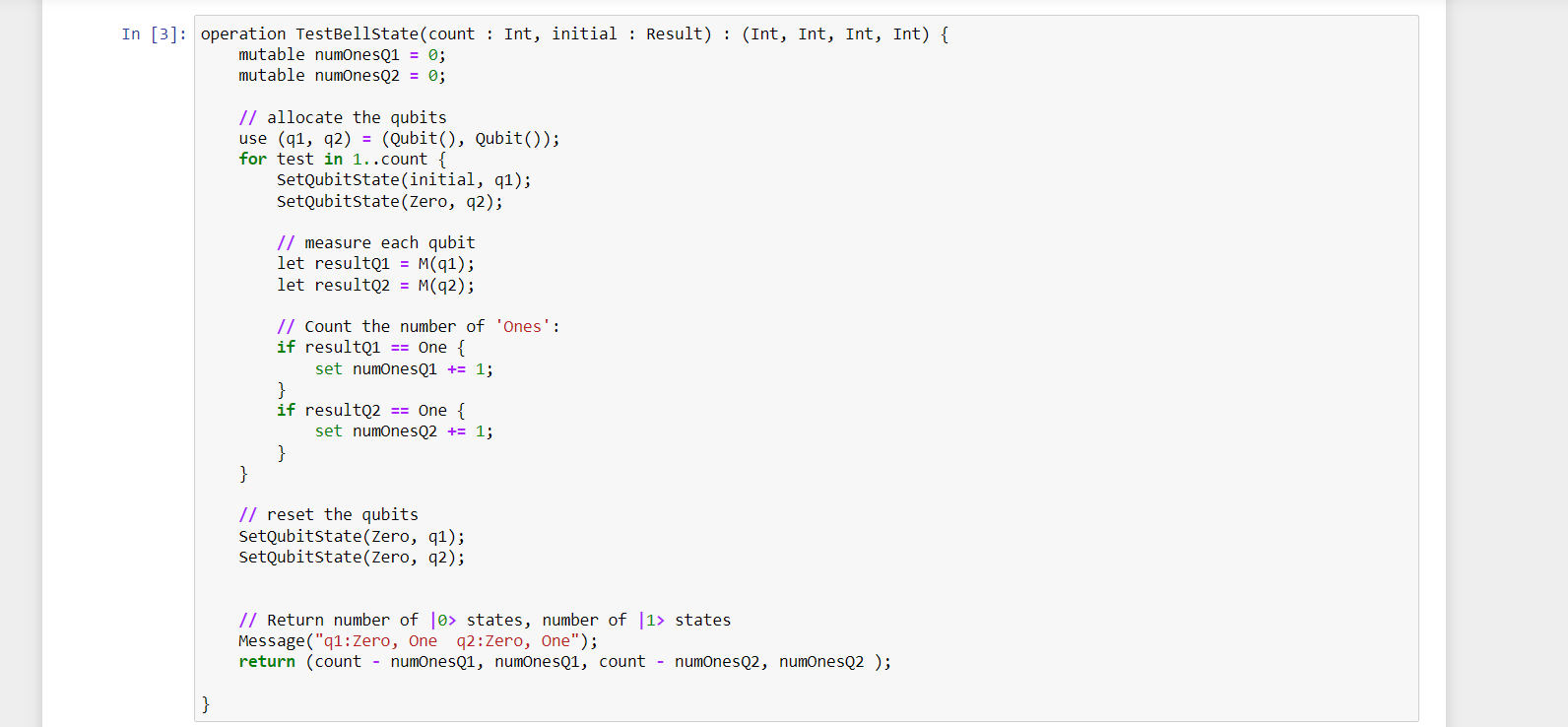
The TestBellState operation:
Test the measurement
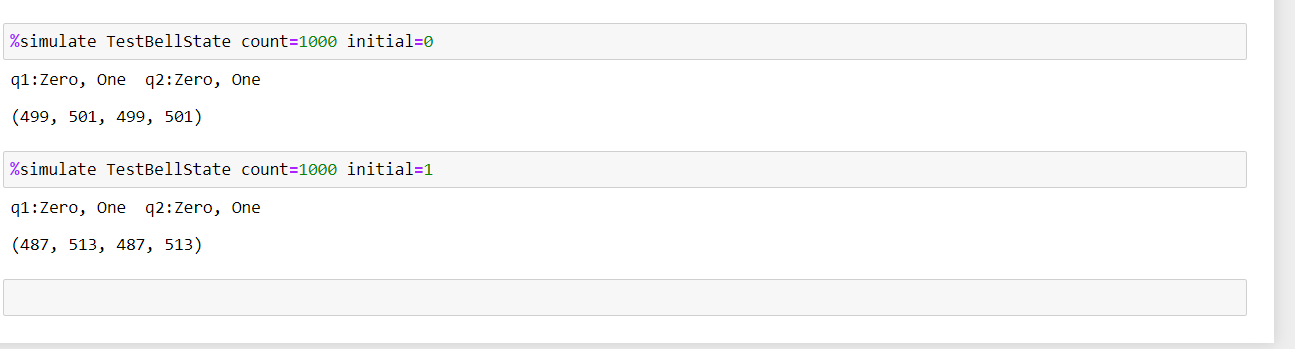
- First we have to take two parameters: "count", which denotes the number of times to run a measurement, and "initial", which denotes the desired state to initialize the qubit.
- Then we will call the "use" statement to initialize two qubits.
- After that we will apply Loops for iteration "count".
And for each loop, it calls SetQubitState to set a specified "initial" value on the first qubit,again Calls "SetQubitState" to set the second qubit to a "Zero"state.
4- Then we will use "M" operation to measure each qubit.
5- And Stores the number of measurements for each qubit that return "One".
After the loop completes, it calls "SetQubitState" again to reset the qubits to a known state (Zero) to allow others to allocate the qubits in a known state. This is required by the "use"statement.
6- Finally, it uses the "Message" function to display a message to the console before returning the results.
Input:
msg : String
The message to be reported.
Output : Unit*
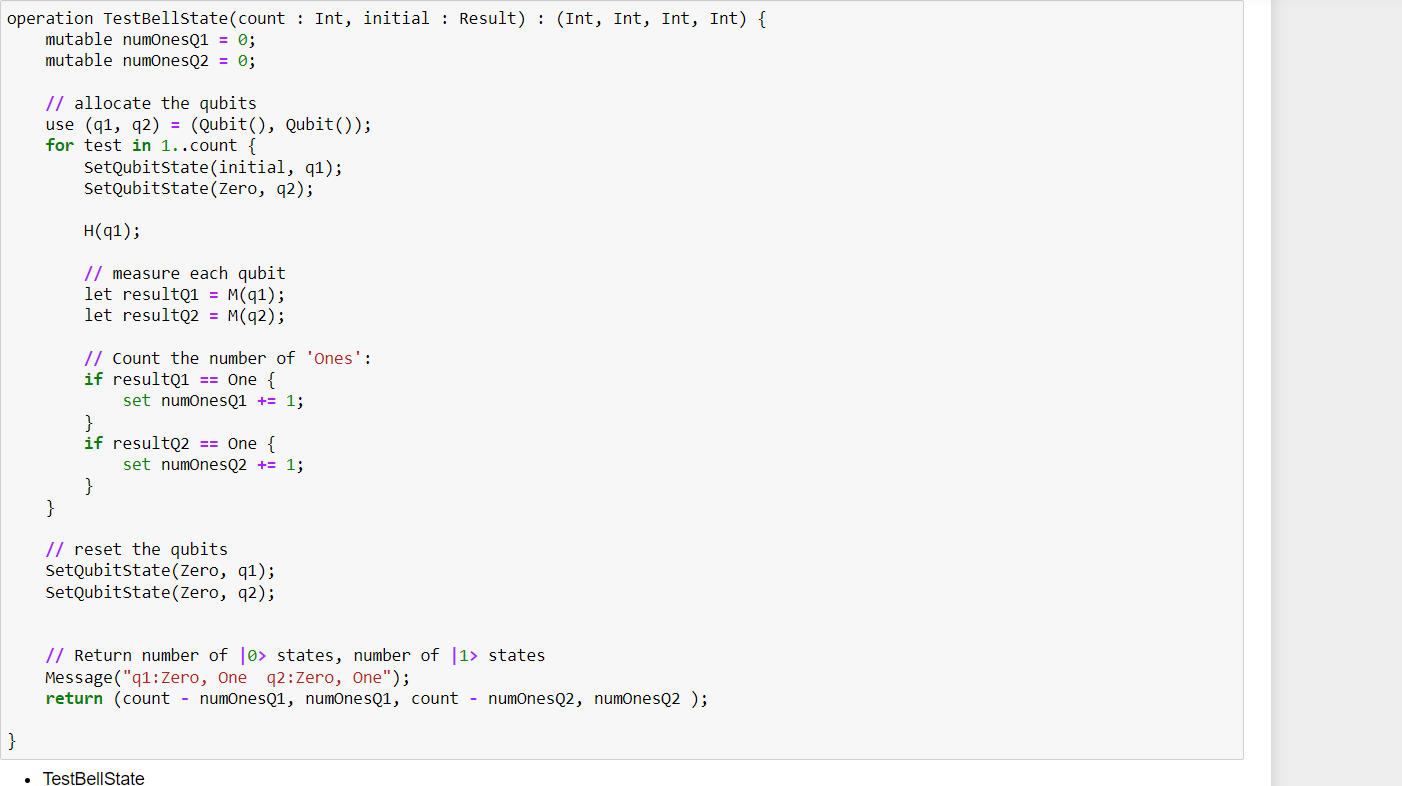
7- Test the code
Test the code up to this point to see the initialization and measurement of the qubits.
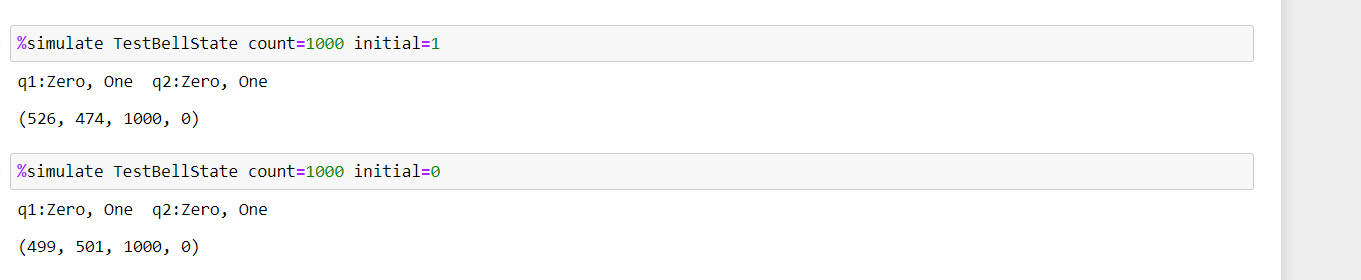
To run the "TestBellState" operation, you use the "%simulate" magic command to call the Azure Quantum full-state simulator. Here we need to specify the "count"and "initial" arguments,
Since the qubits has not been manipulated yet, they have retained their initial values:

Put a qubit in superposition
Before entangling the qubits, you will put the first qubit into a superposition state, where a measurement of the qubit will return Zero 50% of the time and One 50% of the time. Conceptually, the qubit can be thought of as being in a linear combination of all states between the Zero and One.
To put a qubit in superposition, Q# provides the H or Hadamard, operation.
Entangle two qubits
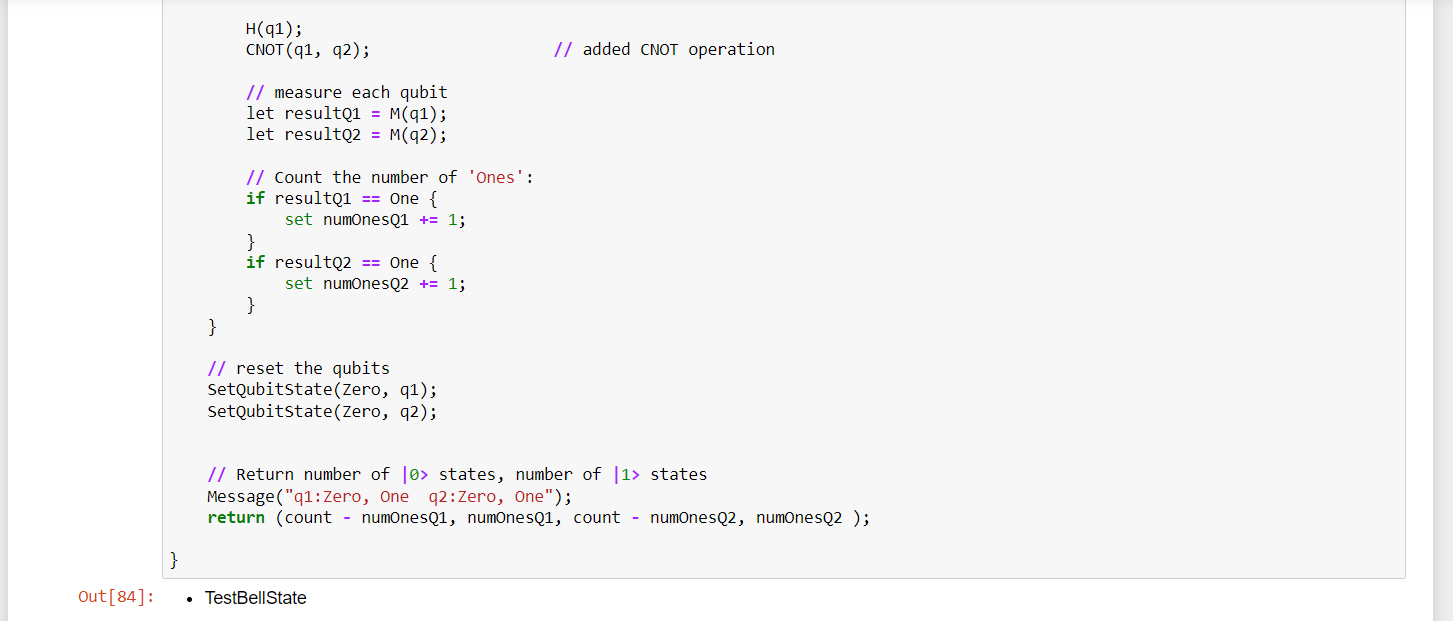
Entangled qubits are connected such that they cannot be described independently from each other. That is, whatever operation happens to one qubit in an entangled pair, also happens to the other qubit.
To enable entanglement, Q# provides the CNOT operation, which stands for Controlled-NOT.
Ex-2 Write and simulate qubit-level programs in Q#
Let's simulate a basic quantum program that operates on individual qubits.
Quantum Fourier Transform(QFT)
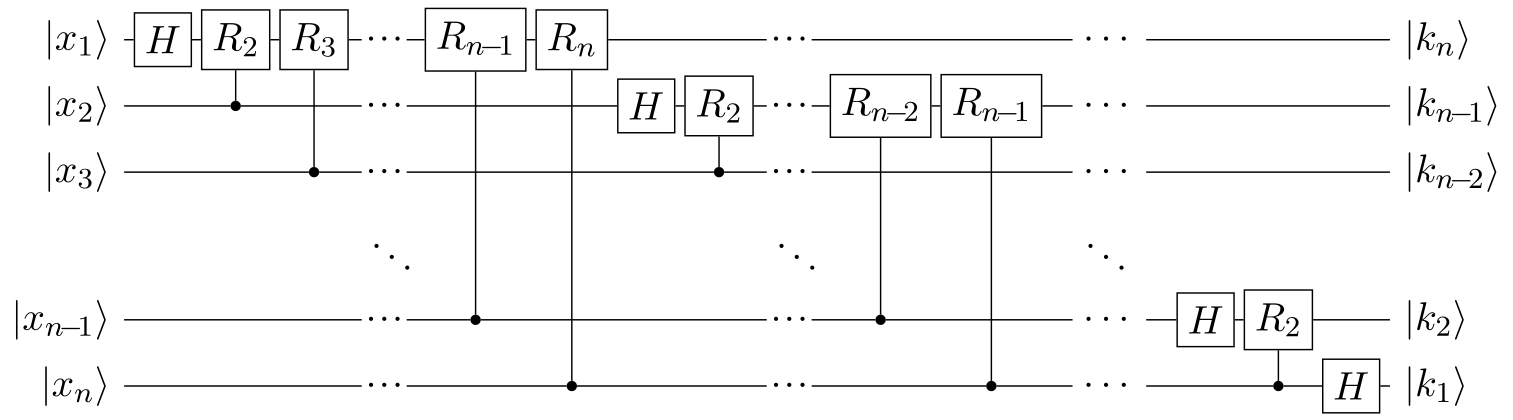
The quantum Fourier transform is a part of many quantum algorithms.The quantum Fourier transform can be performed efficiently on a quantum computer with a decomposition into the product of simpler unitary matrices.
The discrete Fourier transform on 2^n amplitudes can be implemented as a quantum circuit consisting of only Hadamard Gates and controlledphase shift gates, where n is the number of qubits.
Step 1: define the Perform3qubitQFT operation
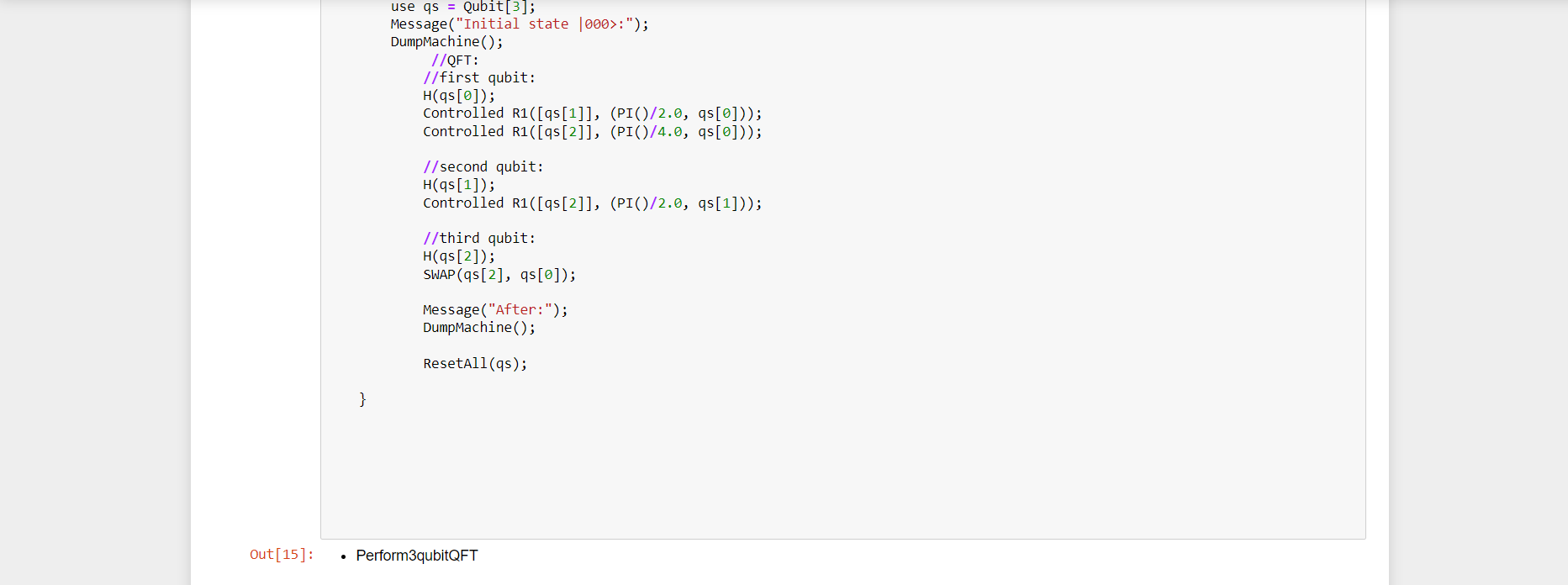
Step 2: allocate a register of three or four qubits with the use keyword
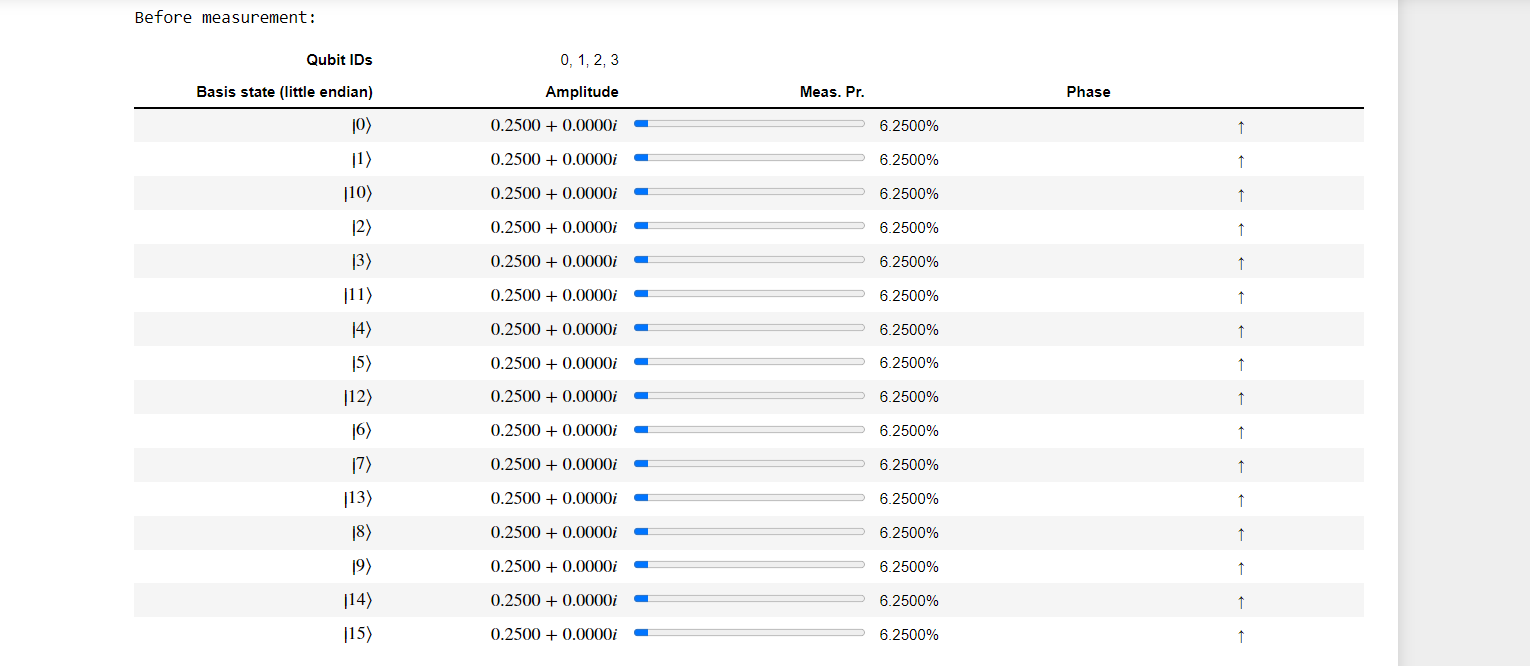
Step3: we can verify their allocated state by using DumpMachine ,which prints the system's current state to the console.
Step4: a) Applying single-qubit
The first operation applied is the H (Hadamard) operation to the first qubit
To apply an operation to a specific qubit from a register , use standard index notation. So, applying the H operation to the first qubit of the register qs takes the form
b) Controlled operations
The QFT circuit consists primarily of controlled R1 rotations. An R1(Theta,qubit) .
So the R1 operations will act on the first qubit (and controlled by the second and third qubits),and so on.
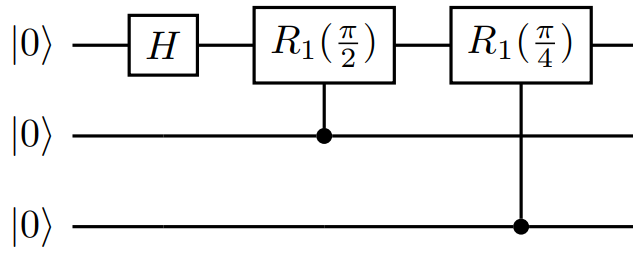
The PI() function is used to define the rotations in terms of pi radians.
After applying the relevant H operations and controlled rotations to the second and third qubits / second,third and fourth qubits.
Step 5 : Then apply a SWAP operation to complete the circuit.
This is necessary because the nature of the quantum Fourier transform outputs the qubits in reverse order.
Step 6: Deallocate qubits
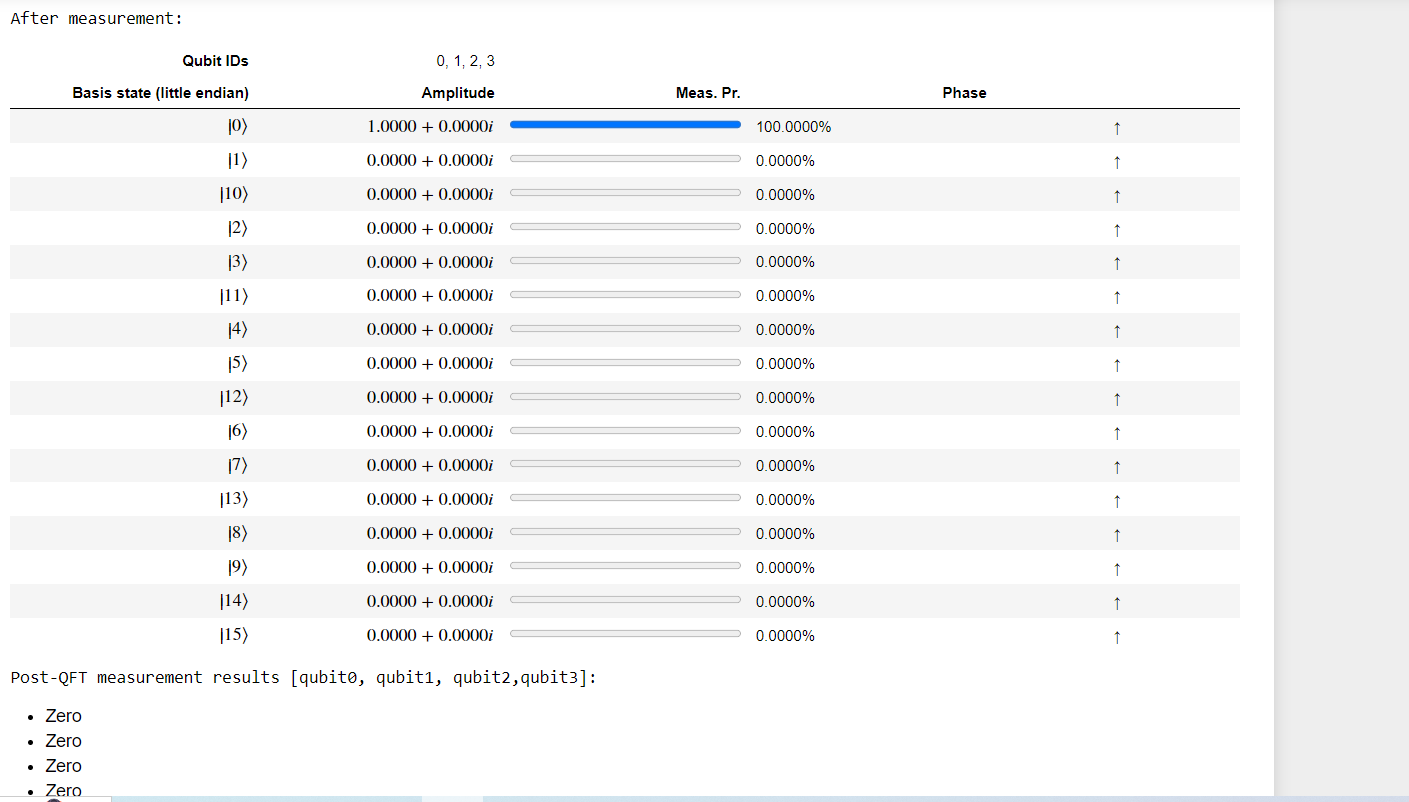
The last step is to call DumpMachine() again to see the post-operation state, and to deallocate the qubits. The qubits were in state |0⟩ when we allocated them and need to be reset to their initial state using the ResetAll operation.
Step 7: Test the operation
Step 8: Understanding the output
When called on the full-state simulator, DumpMachine() provides these multiple representations of the quantum state's wavefunction.
The first row provides a comment with the IDs of the corresponding qubits in their significant order.
The rest of the rows describe the probability amplitude of measuring the basis state vector |i⟩ in both Cartesian and polar formats.
a) With 3 Qubits
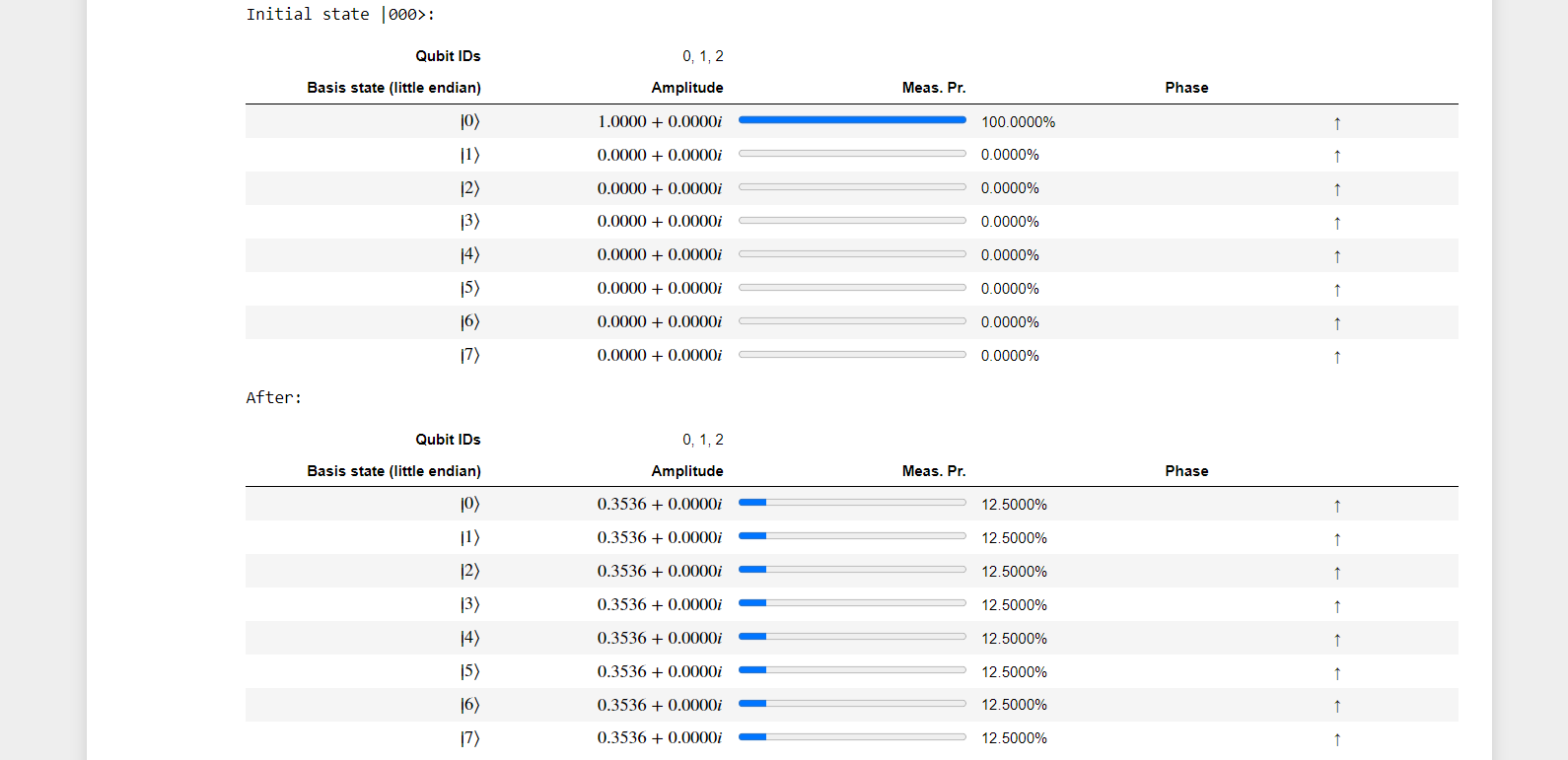
Now let's Modify the operation
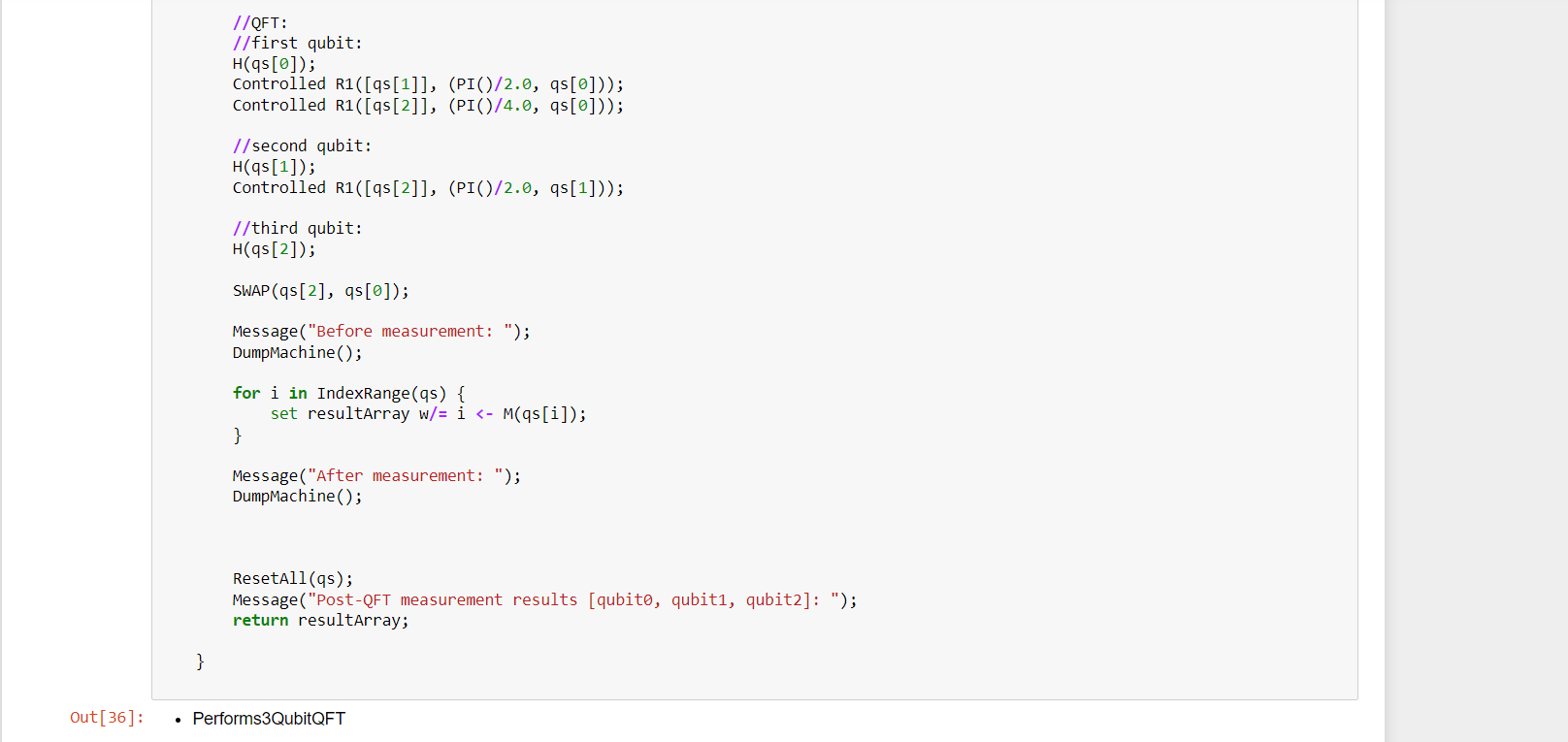
Firstly Define and initialize Result[] array
Lastly , Perform measurements in a for loop and add results to array
With all three qubits measured and the results added to resultArray, you are safe to reset and deallocate the qubits as before.
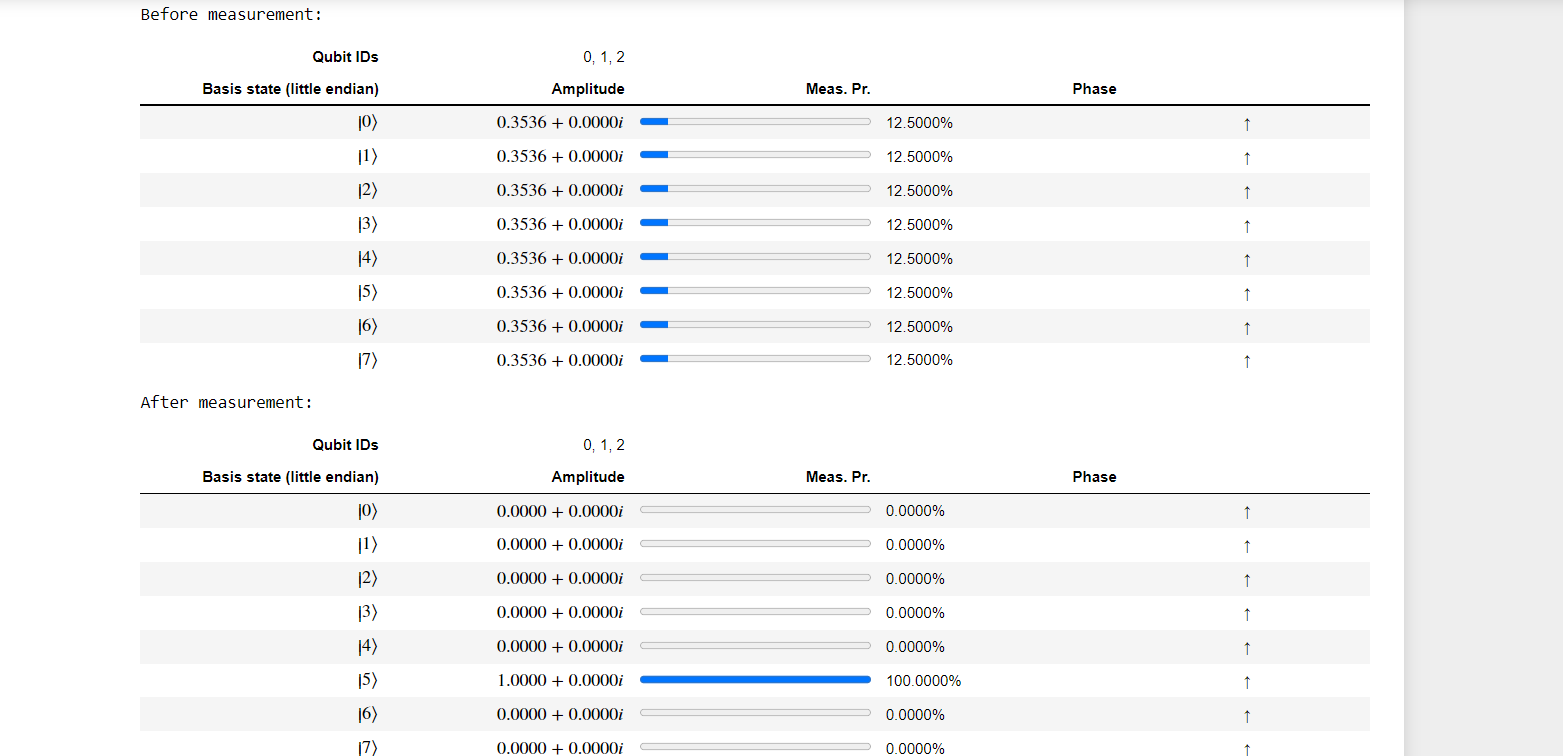

b) With 4 qubits
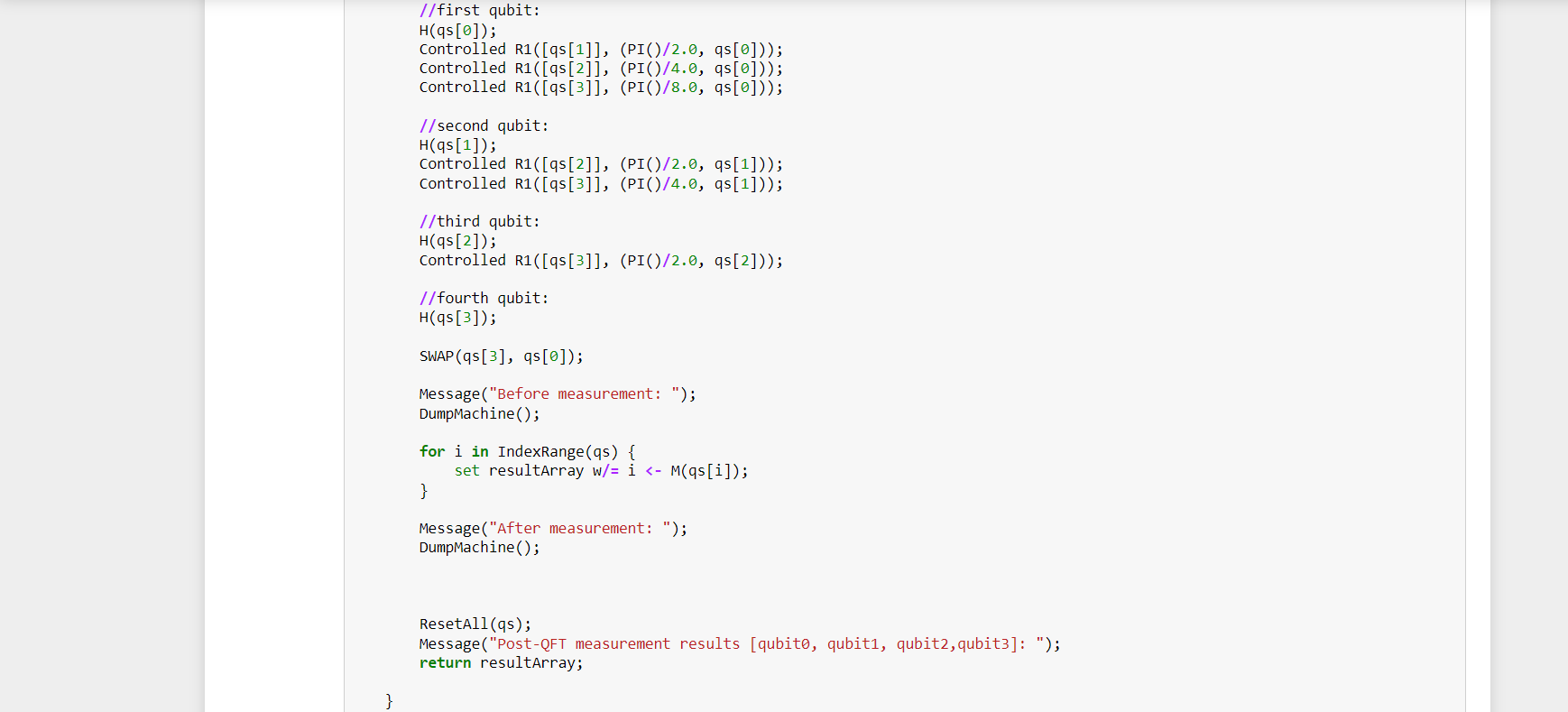

No comments:
Post a Comment